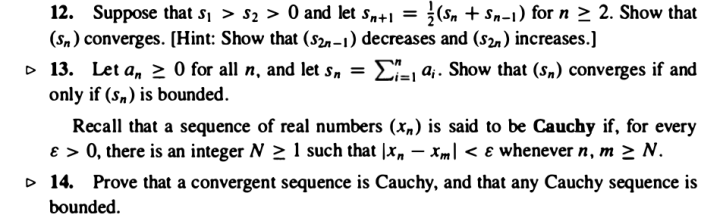Problemas resueltos (Carothers). (8)

Solución:

12. Consideremos las subsucesiones de los términos impares $s_{2n-1}$ y la de los términos pares $s_{2n}$ . Si queremos que la sucesión converja debemos probar que ambas sucesiones convergen y que lo hacen al mismo valor. Estudiamos la sucesión de sus diferencias comenzando con la subsucesión de los términos impares.

Para $n=1$ , resulta $s_{3}-s_{1} = \frac{1}{2} (s_2+s_1)-s_1 = \frac{1}{2} (s_2-s_1) = \frac{1}{2^{2 \cdot 1-1}} (s_2-s_1)$ .

Para $n=2$ , resulta $s_{5}-s_{3} = \frac{1}{2}(s_4+s_3)-s_3 =\frac{1}{2}(s_4-s_3)=\frac{1}{2} (\frac{1}{2} (s_3+s_2)-s_3) =\frac{1}{4} (s_2-s_3) = \frac{1}{4} (s_2-\frac{1}{2}(s_2+s_1)) =\frac{1}{8}(s_2-s_1)=\frac{1}{2^{2 \cdot 2-1}}(s_2-s_1)$

Esto parece darnos una pauta. Conjeturamos que

$s_{2n+1}-s_{2n-1} = \frac{1}{2^{2n-1}} (s_2-s_1)$ . (1)

Probamos por inducción sobre $n$ . Para $n=1$ está ya probado en párrafos anteriores. Sea cierto para $n=r$ . Entonces

$s_{2r+1}-s_{2r-1}= \frac{1}{2^{2r-1}} (s_2-s_1)$ ,

mientras que para $n=r+1$ tenemos que

$s_{2r+3}-s_{2r+1} = \frac{1}{2} (s_{2r+2}+s_{2r+1})-s_{2r+1} = \frac{1}{2}(s_{2r+2}-s_{2r+1}) = \frac{1}{2} (\frac{1}{2} (s_{2r+1}+s_{2r})-s_{2r+1}) = \frac{1}{4} (s_{2r}-s_{2r+1}) = \frac{1}{4} (s_{2r}-\frac{1}{2} (s_{2r}+s_{2r-1}) )= \frac{1}{8} (s_{2r}-s_{2r-1})$ . (2)

Ahora bien, como

$s_{2r+1} = \frac{1}{2} (s_{2r}+s_{2r-1})$ ,

tenemos que

$s_{2r} = 2s_{2r+1}-s_{2r-1}$ .

Sustituyendo en (2), y aplicando la hipótesis de inducción, obtenemos

$s_{2r+3}-s_{2r+1} = \frac{1}{8}(2s_{2r+1}-2s_{2r-1})= \frac{1}{4}(\frac{1}{2^{2r-1}})(s_2-s_1) = \frac{1}{2^{2(r+1)-1}}(s_2-s_1)$ .

Como $s_1 >s_2$ , la sucesión $b_n = s_{2n+1}-s_{2n-1} = \frac{1}{2^{2n-1}}(s_2-s_1)$ es negativa y la subsucesión de los términos impares es decreciente. Para probar que la subsucesión de los términos pares es creciente vamos a escribir las diferencias generales:

$b_n =s_{2n+1} -s_{2n-1} = \frac{1}{2}(s_{2n}+s_{2n-1})-s_{2n-1} = \frac{1}{2}(s_{2n}-s_{2n-1})$ , (3)

$c_n =s_{2n+2}-s_{2n} = \frac{1}{2}(s_{2n+1}+s_{2n})-s_{2n} = \frac{1}{2}(s_{2n+1}-s_{2n})$ . (4)

Observemos que al sumar $b_n$ y $c_n$ resulta

$(s_{2n+1}-s_{2n-1})+(s_{2n+2}-s_{2n}) =\frac{1}{2}(s_{2n+1}-s_{2n-1})$ .

Es decir,

$s_{2n+2}-s_{2n} = -\frac{1}{2} (s_{2n+1}-s_{2n-1})$ .

En símbolos, $c_n = -\frac{1}{2} b_n$ y como $b_n$ es decreciente, resulta que $c_n$ es creciente, con

$s_{2n+2}-s_{2n} = (s_1-s_2) \frac{1}{2^{2n}}$ . (5)

Además, las expresiones obtenidas nos van a permitir dar directamente el valor del límite de dichas subsucesiones. En efecto, sumando desde $k=1$ hasta $k=n$ en (1), resulta

$\sum_{k=1}^{n} s_{2k+1}-s_{2k-1} = (s_2-s_1) \sum_{k=1}^{n} \frac{1}{2^{2k-1}}$ ,

$s_{2n+1} -s_1 = 2(s_2-s_1) \sum_{k=1}^{n} (\frac{1}{4})^{k}$ .

Recordemos la expresión para la suma de una serie geométrica:

$\sum_{k=1}^{n}(\frac{1}{4})^{k} =\frac{(1/4)-(1/4)^{n+1}}{3/4}$

Por tanto,

$s_{2n+1}-s_1 =2(s_2-s_1) \frac{(1/4)-(1/4)^{n+1}}{3/4}$ .

Expresión que llevada al límite resulta

$\lim s_{2n+1} = s_1+ \frac{2}{3} (s_2-s_1)=\frac{1}{3} s_1 +\frac{2}{3}s_2$ .

Del mismo modo, tenemos que sumando desde 1 hasta $n$ en (5)

$\sum_{k=1}^{n} s_{2k+2}-s_{2k} = (s_1-s_2) \sum_{k=1}^{n} \frac{1}{4^{k}}$ ,

$s_{2n+2}-s_2 = (s_1-s_2) \frac{(1/4)-(1/4)^{n+1}}{(3/4)}$ .

Llevando esta última expresión hasta el límite

$\lim_n s_{2n+2} = s_2+(1/3)(s_1-s_2) = \frac{1}{3} s_1 + \frac{2}{3} s_2$ .

En consecuencia, la sucesión $s_n$ es convergente a

$\frac{1}{3} s_1+\frac{2}{3} s_2$ .

13. Sea $s_n = \sum_{i=1}^{n} a_i$ . Como $a_n \geq 0$ , para todo $n$ , resulta que

$s_{n+1} = \sum_{i=1}^{n} a_i + a_{n+1} \geq \sum_{i=1}^{n} a_i = s_n$ ,

y la sucesión es creciente. Si estuviera acotada superiormente sería convergente con límite igual a $\sup_n \{s_n \}$ . Si no está acotada superiormente entonces no tiene límite en la recta real ya que si $l \in \mathbb{R}$ fuera tal límite, tendríamos que para $\epsilon >0$ dado, hallaríamos un entero positivo $n_0$ tal que $s_n \leq l+\epsilon$ si $n \geq n_0$ . Por tanto, tomando

$M = \sup (\{s_n : n < n_0 \} \cup \{l+\epsilon\})$ ,

resultaría que $s_n \leq M$ , para todo $n$ y $s_n$ estaría acotada superiormente en contra de lo supuesto.

14. Supongamos que $x_n$ es una sucesión convergente y que $l \in \mathbb{R}$ es su límite. Entonces para $\epsilon >0$ , hallaremos un entero positivo $N$ , de forma que

$|x_n -l| < \frac{\epsilon}{2}$ ,

si $n \geq N$ . Tomando $n,m \geq N$ , vemos que

$|x_n - x_m| = |x_n -l +l -x_m| \leq |x_n -l|+ |x_m -l| < \frac{\epsilon}{2}+\frac{\epsilon}{2} = \epsilon$ .

Esto prueba que $x_n$ de Cauchy. Supongamos ahora que $x_n$ es de Cauchy. Probaremos que está acotada. En efecto, sea $\epsilon =1 >0$ . Hallaremos un entero postivo $N$ , de forma que si $n,m \geq N$ se tiene

$|x_n - x_m| < 1$ .

Esto significa que haciendo $m=N$ , es para todo $n \geq N$ ,

$-1<x_n -x_N < 1$ ,

$x_N -1 < x_n < 1+x_N$ .

Tomando $U = \sup (\{x_n : n \leq N \} \cup \{1+X_N \})$ y $L = \inf ( \{x_n : n \leq N \} \cup \{ x_N -1 \})$ , vemos que la sucesión está acotada superior e inferiormente por $U$ y $L$ , respectivamente.

Problemas resueltos (Carothers). (8)

Comparte esto:

Relacionado

Deja un comentario Cancelar la respuesta